Prim Algorithm
Prim's Algorithm addresses the problem of finding the Minimum Spanning Tree (MST) in a weighted, connected, undirected graph. The MST is a subset of edges that connects all vertices in the graph with the minimum possible total edge weight.
Prim's Algorithm starts with an arbitrary vertex and grows the MST by iteratively adding the shortest edge that connects a vertex in the MST to a vertex outside the MST. This process continues until all vertices are included in the MST.
function primMST(graph) {
const vertices = Object.keys(graph);
const visited = new Set();
const mst = [];
// Start with an arbitrary vertex
const startVertex = vertices[0];
visited.add(startVertex);
while (visited.size < vertices.length) {
let minWeight = Infinity;
let minEdge;
// Find the minimum weight edge that connects a vertex in the MST to a vertex outside the MST
for (const vertex of visited) {
for (const neighbor in graph[vertex]) {
if (!visited.has(neighbor) && graph[vertex][neighbor] < minWeight) {
minWeight = graph[vertex][neighbor];
minEdge = { start: vertex, end: neighbor, weight: minWeight };
}
}
}
// Add the minimum weight edge to the MST
mst.push(minEdge);
visited.add(minEdge.end);
}
return mst;
}
// Example usage:
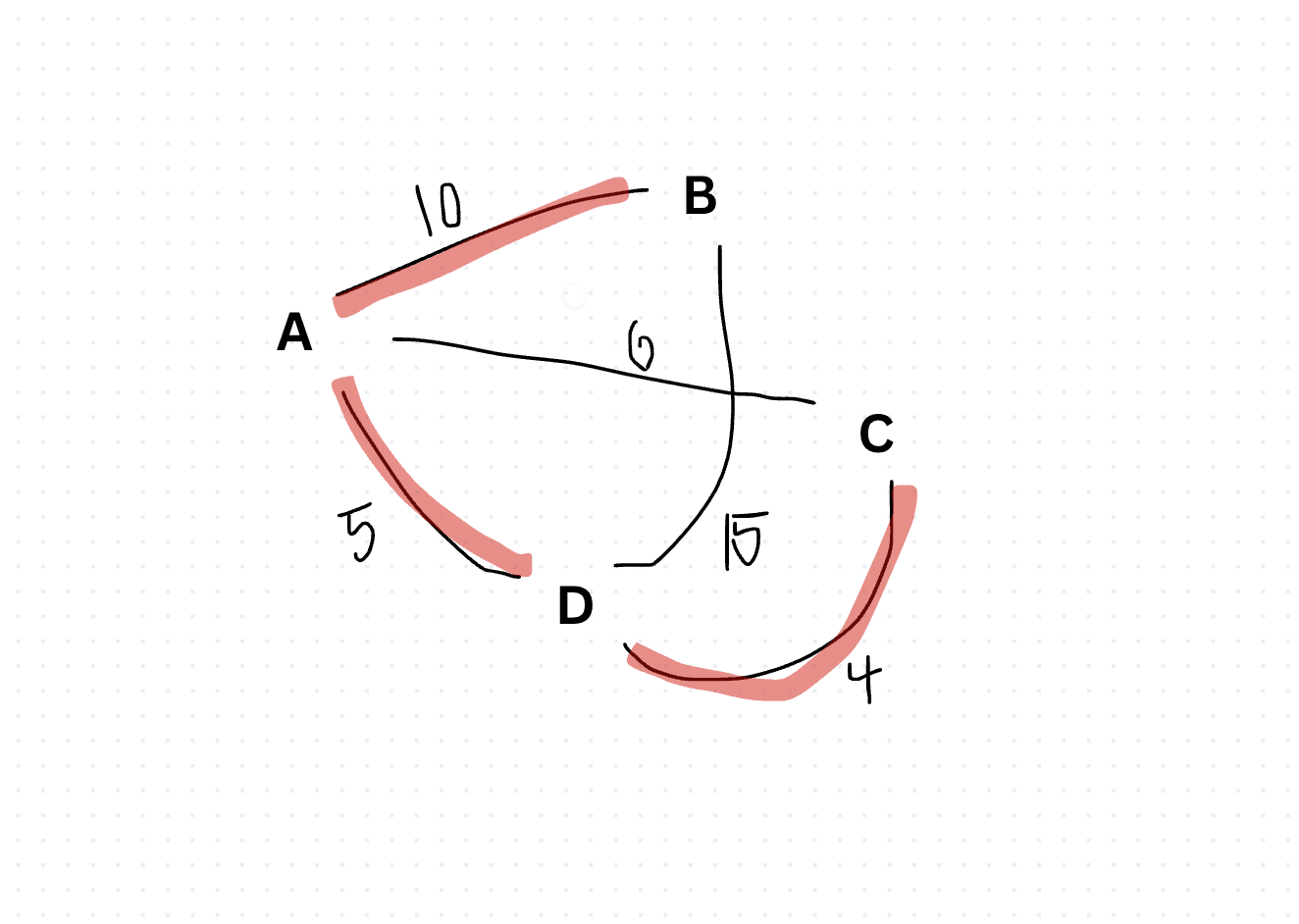
const graph = {
'A': { 'B': 10, 'C': 6, 'D': 5 },
'B': { 'A': 10, 'D': 15 },
'C': { 'A': 6, 'D': 4 },
'D': { 'A': 5, 'B': 15, 'C': 4 }
};
console.log("Minimum Spanning Tree (MST) using Prim's Algorithm:", primMST(graph));Prim's Algorithm finds applications in network design, such as designing communication networks and laying out electrical wiring, where minimizing the total cost or distance is essential.