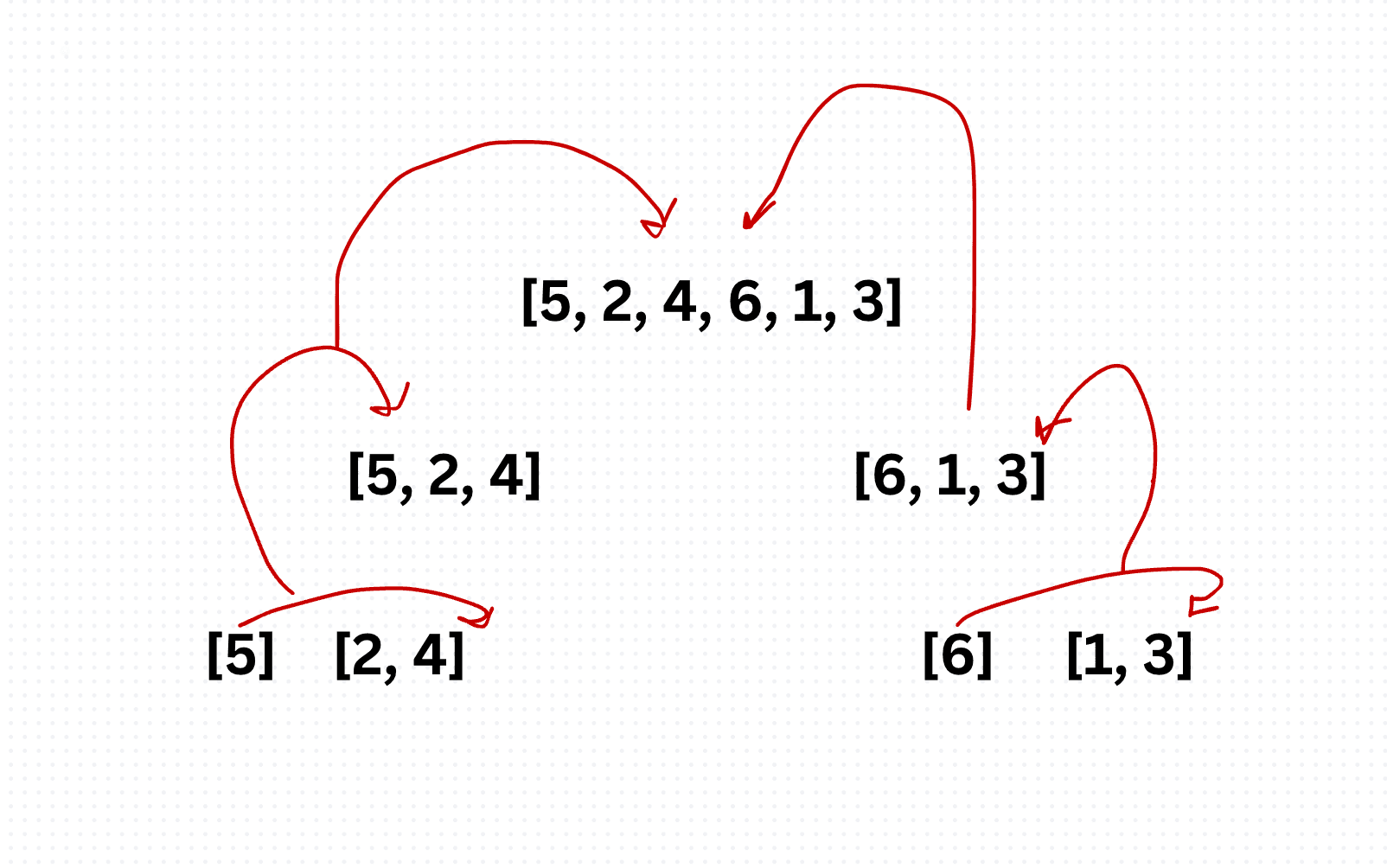
Merge Sort Algorithm

Merge sort splits an array in half, sorts each half, then merges them back together in order. It keeps splitting until every piece is a single element — and a single element is already sorted.

The merge step is where the real work happens. Two sorted arrays get combined into one by comparing their front elements and picking the smaller one each time.

The intuition

Think of sorting a deck of cards. Split the deck in half. Split those halves again. Keep going until you have piles of one card each. Now merge them back: compare the top cards of two piles, put the smaller one down first. Repeat.

The code

function mergeSort(arr) {
    if (arr.length <= 1) return arr;

    const mid = Math.floor(arr.length / 2);
    const left = mergeSort(arr.slice(0, mid));
    const right = mergeSort(arr.slice(mid));

    return merge(left, right);
}

function merge(left, right) {
    const result = [];
    let i = 0;
    let j = 0;

    while (i < left.length && j < right.length) {
        if (left[i] <= right[j]) {
            result.push(left[i++]);
        } else {
            result.push(right[j++]);
        }
    }

    return result.concat(left.slice(i)).concat(right.slice(j));
}

Complexity

• Time: O(n log n) — always. Best case, worst case, average case. That consistency is merge sort's superpower.
• Space: O(n) — needs extra space for the merged arrays.

Trade-offs

Merge sort guarantees O(n log n) regardless of input order. Quick sort is faster in practice (better cache locality, in-place) but has an O(n^2) worst case. Merge sort is also stable — equal elements keep their original order. That matters when sorting by multiple criteria.

The cost is memory. You're creating new arrays at every level of recursion. For massive datasets that don't fit in memory, merge sort shines as the basis for external sorting (sorting data on disk).