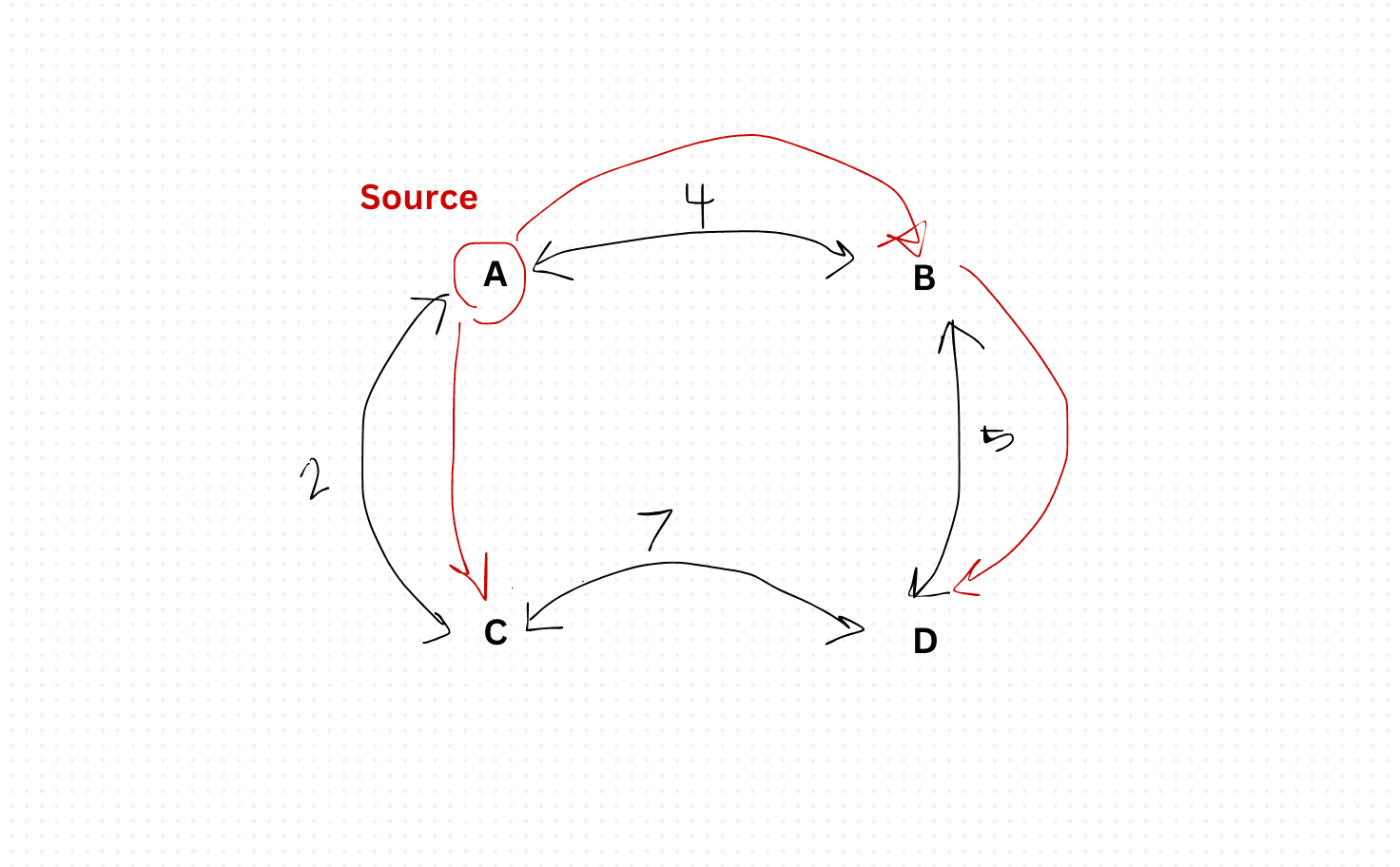
Dijkstra's Algorithm

BFS finds the shortest path when every edge costs the same. But what if edges have different weights? That's where Dijkstra's algorithm comes in.

It finds the shortest path from one node to all other nodes in a weighted graph — as long as no edge weight is negative.

The Intuition

Start at the source. Set its distance to 0 and everything else to infinity. Then, greedily pick the unvisited node closest to the source. For each of its neighbors, check: "Can I reach you faster through this node?" If yes, update the distance.

It's like spreading paint from a source point. The paint always flows through the shortest pipe first.

The Code

function dijkstra(graph, start) {
  const distances = {};
  const visited = new Set();

  for (const node in graph) {
    distances[node] = Infinity;
  }
  distances[start] = 0;

  while (visited.size < Object.keys(graph).length) {
    // pick the unvisited node with smallest distance
    let current = null;
    for (const node in distances) {
      if (!visited.has(node)) {
        if (current === null || distances[node] < distances[current]) {
          current = node;
        }
      }
    }

    visited.add(current);

    for (const neighbor in graph[current]) {
      const newDist = distances[current] + graph[current][neighbor];
      if (newDist < distances[neighbor]) {
        distances[neighbor] = newDist;
      }
    }
  }

  return distances;
}

const graph = {
  A: { B: 4, C: 2 },
  B: { A: 4, D: 5 },
  C: { A: 2, D: 7 },
  D: { B: 5, C: 7 },
};

console.log(dijkstra(graph, 'A'));
// { A: 0, B: 4, C: 2, D: 9 }

Walkthrough

Starting from A:

1. A = 0, B = ∞, C = ∞, D = ∞
2. Visit A → update B to 4, C to 2.
3. Visit C (closest) → update D to 2 + 7 = 9.
4. Visit B → D through B = 4 + 5 = 9 (not better).
5. Visit D → done.

Shortest paths from A: B = 4, C = 2, D = 9.

Complexity

• Time: O(V²) with the simple version above. O((V + E) log V) with a priority queue.
• Space: O(V) for the distances and visited set.

The Trade-off

This simple implementation scans all nodes to find the minimum distance each step — that's the O(V²). For large graphs, use a min-heap (priority queue) to bring it down to O((V + E) log V).

Dijkstra breaks with negative edge weights. If any edge has a negative cost, use Bellman-Ford instead (O(V·E), but handles negatives).