The Binary Search Algorithm is a fundamental search algorithm used to efficiently find a target element within a sorted array. In this article, we'll delve into the workings of this algorithm, its implementation in JavaScript, and its time complexity analysis.

Binary search is a divide-and-conquer algorithm that repeatedly divides the search interval in half until the target element is found (or determined to be absent). It works by comparing the target value with the middle element of the array. If the target value matches the middle element, the search is complete. If the target value is less than the middle element, the search continues in the lower half of the array. If the target value is greater than the middle element, the search continues in the upper half of the array.

Here's a simple implementation of the binary search algorithm in JavaScript:

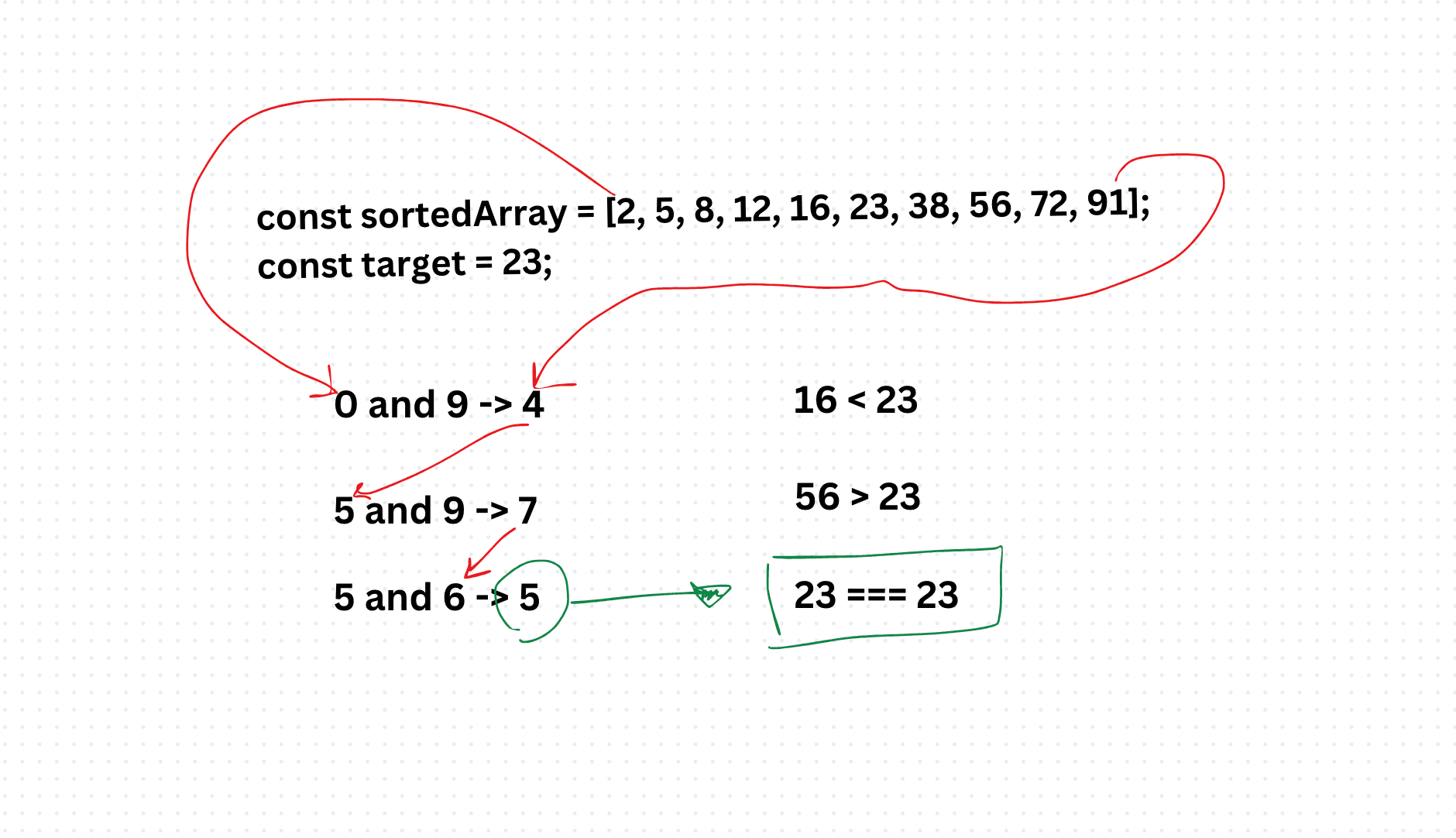
const sortedArray = [2, 5, 8, 12, 16, 23, 38, 56, 72, 91];
const target = 23;

const binarySearch = (myArray, myTarget) => {
    let left = 0;
    let right = myArray.length - 1;

    while (left < right) {
        const mid = Math.floor((left+right) / 2)
        if (myArray[mid] === target) {
            return mid;
        } else if (myArray[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return -1;
}

console.log(binarySearch(sortedArray,target))

In this example, we have a sorted array sortedArray and a target value target. We use the binarySearch function to find the index of the target value in the array. If the target is found, we print its index; otherwise, we indicate that the target is not present in the array.

Conclusion:

Binary search is a powerful algorithm for efficiently searching sorted arrays. Its logarithmic time complexity of O(log n) makes it ideal for large datasets. By dividing the search interval in half at each step, binary search quickly converges to the target value, making it a fundamental tool in computer science and algorithmic problem-solving.